What's an Assist Really Worth?

Part 1: Getting to the Root of Assists

A couple weeks ago I stumbled onto the Numbers Guy blog at the Wall Street Journal, and added it to my Google Reader. One of the posts in the archive reminded me of something I've been meaning to write about for quite some time: how I deal with assists in the calculation of PAPER.

Since PAPER isn't a linear weights system in which each event has a positive or negative value, I've never been too much concerned with the point-value of an assist. Knowing the difference between the likelihood of making an assisted shot versus a non-assisted one, however, is important. To that end, I compared Field Goal Percentage and Assists:Attempts for all regular-season conference games in the four-season period between 2003 and 2006 and came up with the following (click on the graph to see a larger version):

In the average ACC game in that period, there would be about 6 additional field goals scored for every 10 assists a team racked up. Note that I didn't say the assists led to the baskets being scored; since on a team level, assists are just a subset of field goals made, the assists don't cause the extra baskets to be made. Something else does--something that isn't listed in the box score--and it's something we've got to guess at.

We know the field goal percentages, and we know how many assists were recorded. The fourth critical piece of information if we're going to have any hope of valuing assists properly is the number of times shots were taken on which an assist would have been recorded had the shot been made, regardless of whether or not the shot went into the basket. I call this fourth number the Setup. If we can determine how many Setups occurred, we can find two different field goal percentages for each team: Setup FG% (Assists divided by Setups), and Solo FG% (Field Goals Made minus Assists, divided by Field Goal Attempts minus Setups).

Using the information above, we can see that a team with an Assist-to-Attempt ratio of 0.10 would have an expected field goal percentage of .357; improving that ratio to 0.50 would give an expected field goal percentage of .600. Assuming that both Setup and Solo FG% remain constant, their respective values must be .755 and .297.

Obviously, though, that's an average. Shooting prowess varies from team to team, so those are hardly one-size-fits-all numbers. What's needed is a framework by which we can infer the Setup rates of each team. While it would be tempting to use the ratio of Setup to Solo FG%, which is about 2.5-to-1, that would give an impossible Setup FG% greater than 1 for any Solo FG% greater than .400. Likewise, simply applying the difference of about .46 would break down at Solo FG% greater than .540.

The solution I came up with was to estimate Setup FG% to be the cube-root of Solo FG%, and the red line on the above chart represents the cube-root best-fit line for league-average in the study. While not quite perfect, using the cube-root method has the advantage of never breaking down for any FG% between 0 and 1. Using the cubic formula, we can estimate the number of Setups (S) for any team as long as we know how many field goals they made (M) and attempted (T) and how many assists (A) were recorded as follows:

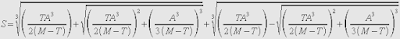That looks like an awful lot to keep track of, but it's a fairly simple equation to build into a database or spreadsheet function.

Coming up in Part 2: What does all this allow us to do?